بخش مکعب رنگی در قسمت هوش آزمون یوس

همان گونه که می دانید ریاضی، هندسه و هوش سه مبحث اصلی ای هستند که در آزمون یوس از آن ها سوالاتی پرسیده می شود. در این نوشته به توضیح درمورد مباحث هوش یوس و از میان مباحث آن به مبحث مکعب رنگی می پردازیم. تسلط کافی بر این مباحث تا حدود زیادی موفقیت شما را در پذیرش در این آزمون تضمین می کند. بخش هوش آزمون یوس به سوالات سنگینی که نیاز به محاسبه های پیچیده و زمان بر دارند، نمی پردازد. بلکه بیشتر بر سنجش توانایی تجزیه و تحلیل داده های داوطلبان و تجسم سه بعدی آن ها متمرکز است. معمولا نمی توان سرفصل های مشخصی برای این بخش آزمون یوس تعریف کرد و هر کدام از دانشگاه های ترکیه خودشان این مباحث را مشخص می کنند.

با این حال شما می توانید با مراجعه به سایت یونی لند، سرفصل های مشخص شده ای را بیابید. برخی از آن ها عبارت اند از کد گذاری ها و پسورد، روابط بین اشکال (دوران، تقارن، قیچی و …)، تاس، سری های عددی، جدول های اپراتوری، جدول های خاص (سودوکو، ربع جادویی و …)، اشکال اپراتوری و … .

توضیحات کلی درمورد مکعب ها

مکعب های مختلف، دارای گوشه، ضلع (طول، عرض، ارتفاع) و مساحت هستند. برای مثال یک مکعب مستطیل 8 گوشه، 12 ضلع و از نظر مساحت نیز 6 وجه دارد. با استفاده از این اطلاعات می توان در سوالات مختلف تعداد مکعب ها را شمرد. اگر تمام قسمت های مکعب قابل مشاهده باشد، با شمارش عادی می توان به جواب دست یافت. اگر سوراخ داشته باشند نیز به دو روش می توان تعدادشان را شمرد. در روش اول از روش عادی استفاده می کنیم و در نهایت تعداد سوراخ ها را از آن ها کم می کنیم و در روش دوم شکل را از بالا تصور می کنیم و با در نظر گرفتن سوراخ ها تعداد مکعب ها را به دست می آوریم. در ادامه مبحث مکعبات رنگی را به تفصیل توضیح می دهیم.

مکعب های رنگی چه مکعب هایی هستند؟

بیشتر سوالات در این زمینه را به نوعی مطرح می کنند که گویی یک سازه مکعبی (مانند آنچه که تا کنون بررسی شد) در یک سطل رنگ فرو رفته، به آن آغشته شده و تمام سطح خارجی اش، رنگی شده است. بدیهی است که در این حالت، رنگ با لایه های درونی و مکعب های داخل سازه مکعب رنگی برخوردی نداشته و تنها سطح جانبی آن مد نظر ما است. هر مکعب کوچک در یک سازه به طور طبیعی دارای 6 وجه است؛ اما تمام آن ها رنگی نمی شوند. در ادامه نحوه بررسی وجوه رنگی توضیح داده خواهد شد.

وجوه رنگی مکعب ها از چه راهی مشخص می شوند؟

در قدم اول باید تعداد وجوه خارجی مشخص شوند. این تعداد برای ما تعیین می کند که در هر مکعب سازه با توجه به نحوه قرارگیری و چینش مکعب های کوچک در کنار دیگر مکعب ها، کدام وجوه، وجوه بیرونی محسوب می شوند و در تماس با رنگ به آن آغشته می شوند.

اگر بخواهیم این مورد را با روشی آسان توضیح دهیم، بهتر است بگوییم که اگر یک مکعب را به تنهایی در سطل رنگ غوطه ور کنیم، تمام 6 وجه آن رنگی می شود. حال اگر دو عدد را به هم بچسبانیم، وجوه رنگی مکعب رنگی چگونه محاسبه می شود؟

روشی که ما پیشنهاد می دهیم به این صورت است:

تعداد کل وجوه – تعداد وجوهی که به مکعب بعدی چسبیده است.

هر کدام از این دو مکعب 6 وجه دارند که از میانشان تنها 1 وجه به مکعب بعدی چسبیده است.

مکعب اول: 6 – 1= 5

مکعب دوم: 6 – 1= 5

در مجموع 10 وجه این دو مکعب رنگی می شوند.

حال حالتی را تصور کنید که سه مکعب به یکدیگر چسبیده اند و ما می خواهیم تعداد وجوه خارجی آن را به دست آوریم. بدیهی است که از این سه، دو مکعب رنگی تنها به یک مکعب وصل شده اند. به عبارت ساده تر، یک مکعب دو مکعب دیگر را به یکدیگر وصل کرده است. این دو مکعب مانند حالت قبل هر کدام 5 وجه رنگی دارند. نکته مهم درمورد مکعبی است که در وسط واقع شده و از دو سوی به مکعب های دیگر چسبیده است. در این حالت از 6 وجه آن عدد 2 را کم می کنیم. عدد به دست آمده، یعنی 4، به ما نشان می دهد که از 6 ضلع، 4 ضلع آن رنگی می شوند.

در مجموع مانند مورد قبل تعداد وجوه خارجی هر مکعب را با یکدیگر جمع می کنیم و به جواب صحیح می رسیم:

5 + 5 + 4 = 14

با توجه به موارد گفته شده می توانیم به این نکته مهم برسیم که هر چه مکعب رنگی کوچک در مرکز سازه قرار داشته باشد و سطح مشترک بیشتری با مکعب های دیگر داشته باشد، تعداد وجوه خارجی آن کمتر می شود. خلاف این موضوع نیز صادق است. هر چقدر مکعب های کوچک به سمت بیرون متمایل باشند، در گوشه سازه قرار بگیرند و سطح مشترک کمتری با دیگر مکعب ها داشته باشند، سطح بیشتری از آن ها به رنگ آغشته می شود.

نحوه محاسبه وجوه رنگی مکعب 3 در 3

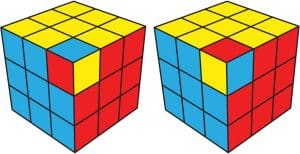
اکنون مکعب 3 در 3 ای را در نظر بگیرید که قرار است وجوه رنگی آن را به دست آوریم. مکعبی که در گوشه بالا سمت راست قرار می گیرد، از سه جهت پایین، چپ و راست به مکعب های دیگر متصل شده است؛ در نتیجه تنها سه ضلع آن رنگی می شوند.

پیشتر اشاره کردیم که مکعب های گوشه ای، بیشترین وجه رنگی را دارند؛ بنابراین عدد به دست آمده از هر مکعب کوچک، نمی تواند بیشتر از 3 باشد. از این رو مکعب هایی که در گوشه ها قرار دارند، سه وجه شان رنگی است و در یک مکعب 3 در 3، 8 گوشه مشاهده می شود.

مکعب هایی که در لبه ها قرار دارند نیز دارای دو وجه رنگی هستند. در هر ضلع، یک مکعب دو لبه ای قرار دارد و هر مکعب 3 در 3 دارای 4 عرض، 4 طول و 4 ارتفاع است؛ بنابراین در آن 12 مکعب رنگی دو لبه ای می توان دید.

برای به دست آوردن مکعب های یک وجه رنگی باید مرکز وجوه را در نظر گرفت. در این حالت یک لایه کامل از دور هر وجه را کنار می گذاریم؛ در نتیجه در یک وجه، یک مکعب یک لبه رنگی باقی می ماند. تمام وجوه مکعب مربع مشابه یکدیگر اند؛ بنابراین 6 عدد مکعب یک وجه رنگی به دست می آید.

مکعب 3 در 3 در مجموع از 27 مکعب کوچک تشکیل شده است. از این 27 مکعب، 26 عدد آن ها را بررسی کردیم (8 + 12 + 6 = 26). یک عدد مکعب باقی می ماند که در مرکز سازه قرار دارد و هیچ کدام از وجوه آن رنگی نشده اند. به این مکعب در اصطلاح، پِینت لِس paintless یا بدون رنگ گفته می شود.

جمع بندی

تمام این نکات مهم در فیلم های آموزشی رایگان یونی لند با عنوان « هوش|دوره بهاره|مکعب|مکعب رنگی » بررسی شده اند و شما می توانید با مراجعه به این سایت و مشاهده مطالب کارآمد و حرفه ای آن، شانس خود را در موفقیت در بخش هوش آزمون یوس بالا ببرید.